Fischers Höhensatz
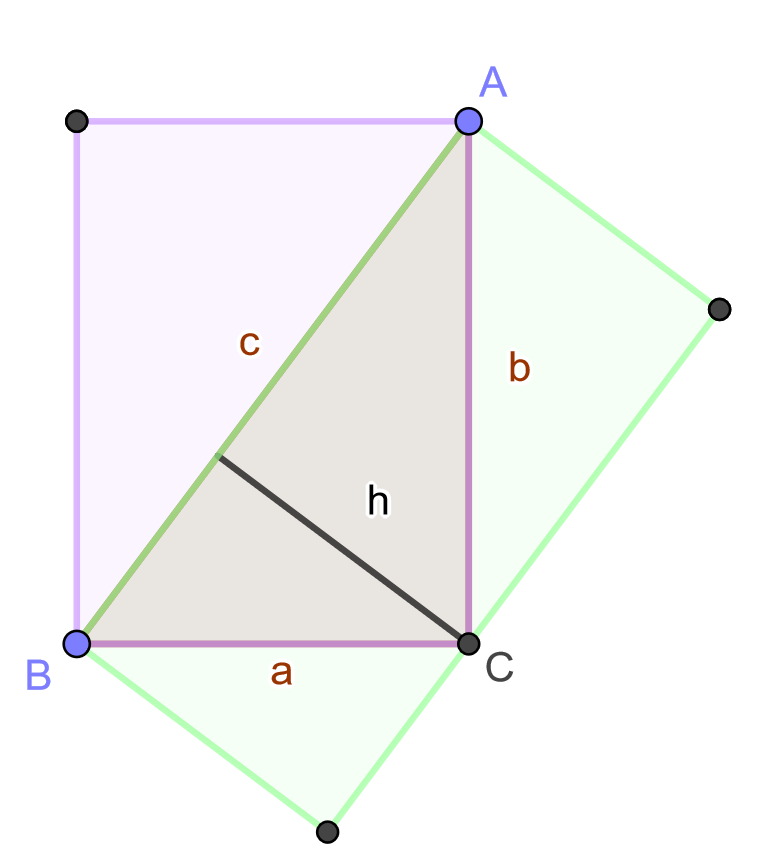
Ein Dreieck mit der Hypotenuse c und ihrer Höhe h ist genau dann rechtwinklig, wenn gilt: h = a·b/c.
Beweis:
½ h·c = ½ a·b
h·c = a·b
h = a·b/c
Bedeutung:
Mit diesem Satz bildet die Satzgruppe des Pythagoras ein geschlossenes Beweissystem, in dem nichts mehr „vom Himmel fällt“.
Allgemeines Dreieck: Fischers Flächenformel
Bei Wikipedia findet sich einerseits der Satz des Heron, der hier nicht unterschlagen werden soll:
A = √(s(s-a)(s-b)(s-c)) , wobei s = ½(a + b + c)
Der neue Satz lautet: A = ¼√(4a²b² − (a² − b² + c²)²)
Ein Vorteil gegenüber Heron: Die Formel ist mit einem Schritt berechenbar und deshalb maschinell einfacher verwertbar. Die Bezeichnungen der Seiten lassen sich symmetrisch vertauschen. Der Beweis wird nachgereicht.
Ableitung ohne Grenzwertbegriff
Vorbemerkung: Das Thema klingt mächtig nach mathematischer Esoterik. Die Versuche mathematischer Querdenker, das Unendliche aus der Mathematik aus weltanschaulichen Gründen zu tilgen, teile ich - als Theologe (!) - in keinster Weise. Andererseits ist das spielerische Hantieren mit Erkenntnissen eine der primären Initialmethoden von Mathematik - und mein Ur-Antrieb, Mathematik zu treiben. Nichts, was "wahr" ist, kann unmathematisch oder Häresie sein!
Die Steigung einer Parabel in einem Punkt
Die Steigung einer Parabel in einem Punkt wird zumeist identifiziert mit der – leichter zu definierenden bzw. zu bestimmenden – Steigung ihrer Tangente in diesem Punkt. Die Tangente ist nun die Gerade, die mit der Parabel in P(x0|f(x0)) einen Berührpunkt hat. Bildet man die Differenz aus quadratischer Funktion f und linearer Tangentenfunktion t, so ergibt sich
f(x0) – t(x0) = 0 besitzt eine doppelte Nullstelle in x0:
f(x) – t(x) = 0 ⇔ x1,2 = m/2 ± √(m2/4+n)
Da die beiden Nullstellen in x0 liegen, gilt m/2 = x0 ⇔ m = 2x0
Die Ableitungsfunktion der Elementarparabel ist damit f'(x) = 2x. Ohne Grenzwertbegriff.
Verallgemeinerung des Verfahrens auf ganzrationale Funktionen 3. Grades
ObdA.: f(x) = x³
⇒ x3 − mx − n = (x − x0)2 · Restpolynom
= (x2 − 2xx0 + x02) · Restpolynom
= (x2 − 2xx0 + x02) · (x + Zahl)
= x3 − 2x2x0 + xx02 + x2·Zahl − 2xx0·Zahl + x02·Zahl = x3 − x2(2x0 − Zahl) + x(x02 − 2x0·Zahl) + x02·Zahl
⇒ 2x0 = Zahl
Die Zeile 2x0 = Zahl ergibt sich daraus, dass die x²-Terme in der Zeile darüber verschwinden müssen.
⇒ x02 − 2x0·Zahl = −m
Denn −m ist der Koeffizient von x in der Ausgangsgleichung (Koeffizientenvergleich)
⇒ m = 3x02 ⇒ f'(x) = 3x2
Damnit sind alle notwendigen Ideen geboren und die Konsequenzen absehbar!